Filters For the 0 - 3 GHz
Spectrum Analyser
Notes:
Resolution filters (Final Crystal Filters)
Just over a year ago, many of us took advantage
of the very generous offer to obtain the sets of crystals to
build the resolution filters. Scotty followed this up with a
note describing the nature of the crystals together with a
warning concerning the fragility of the leads. These leads are
very delicate and WILL break if you try to bend them more than
once. Just very carefully straighten them and then solder them
onto the board. Believe me, I broke two leads on my first
attempt but managed to solder through the plated through holes
to rescue the filter.
The excellent program Dishal 203 will guide you through the
design stage but assumes that all crystals are the exactly same
so be prepared to experiment with values. I used at least two
caps for each value, one at about 75-80% of the target value
and the other selected on test. To make it easier to change the
caps, I solder two short pieces of wire (scraps from wire ended
resistors) at each location and solder the C's to these until I
get the best result. Then remove the wires and solder the SAME
C's in their final place. You have in effect eleven C's and two
L's to play with so be prepared to spend some time to get it
right. The computer program will give you the filter impedance
but do not assume that the circuits connected to the filter are
50 ohm, they will be close but will require tweaking to get the
response correct. I found that the maximum bandwidth that
Dishal designs for is about 7kHz so I am going to have to
resort to commercial units to get the wider bandwidths. I
haven't built the very narrow filter yet but I am aiming for
about 500Hz. If anyone knows if greater bandwidths can be
obtained using the sets supplied, please pass on how it can be
done.
Good luck
Geoff
--------
If you just want a filter that can let you determine whether
everything else is basically functional, you can build a 60 kHz
bandwidth filter very simply, by cascading two ceramic filters
and adding impedance matching components. The results are shown
here:
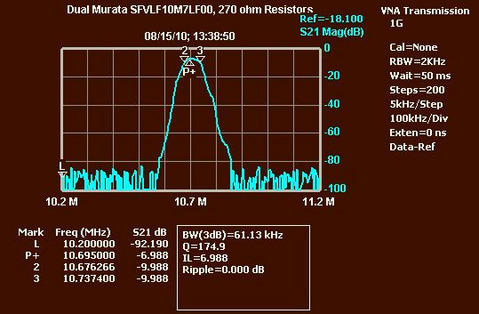
That image used resistors to match, but you would want to use
1.8 uH inductors (Q of at least 20) leading to the filters and
100 pF shunt to ground at the filter terminals. You likely
could get by without any fine tuning, though you would probably
want to tune it later.
The wide filter limits the resolution of your scans, but there
is very little chance that its shape will come out totally
wacko, so it at least lets you see whether the rest of the MSA
works. And when you have a full set of RBW filters, this can be
one of them.
For narrower filters, a simple way to get started is to buy a
canned filter on eBay, such as this one:
eBay filters don't always specify the terminating impedance,
but this one does. The termination is specified as 2000
ohms,which you would match to 50 ohms with 4.7 uH inductors
leading to the filter terminals and 47 pF capacitance shunt to
ground from the terminals. To allow some tuning, use 33 pF
capacitors and a small trimmer that goes to 25 pF or so. You
don't need any equipment to tune it other than the MSA. Just
install it as the RBW filter, and do a sweep with center=0 and
span=0.02 MHz and you should get a nice graph of the top 50 dB
or so of its response, which is all you need for tuning. Adjust
the trimmers until the top of the response looks good.
For a PCB, you can use a blank double-sided board. Drill holes
for the terminals and for a few ground vias. Mount the filter
on the bottom and solder its case to ground. Put the components
on the top with a fence running across the middle of the filter
to isolate the input and output. Solder a fence around the
outside of the board and solder a lid on it to cover the
components. (If the fence is soldered to both the top and
bottom ground planes, you can skip the ground vias described
above.) It is not critical to solder the lid to the isolation
fence in the middle of the filter. Poke/drill/cut two holes in
the lid so you can tune the trimmers. You can cover the holes
later with copper tape (or tack on a piece of brass), though it
doesn't seem to cause any harm to leave them open.
I forgot the SMA connectors. Poke holes in the enclosing fence
and solder the connectors to the fence with the center pin
poking through the hole. A filter built with a similar approach
is shown here:
-----------
Crystal Ladder Filters
I have not actually built a crystal ladder filter, but I have
tested some crystals and used the results to simulate some
filters. I'm looking at bandwidth in the 500-1000 Hz range.
Before I started playing with the simulations, I assumed that
getting a good response with a narrow bandwidth might require
more crystals than for a wider bandwidth. Exactly the opposite
seems to be the case, as the simulation results are very good
for a 800 Hz filter with 4 crystals and a 500 Hz filter with 3
crystals. This is good news, as the smaller number of crystals
obviously simplifies crystal matching and tuning of the
assembled circuit.
Another interesting simulation experiment: I used 5 crystals
and did away with all the series and shunt capacitors and put
unity gain buffer amps between the stages. Four amps total--no
amp at input and output. I made the source and load 50 ohms.
Then I put a 100 ohm load at the output of each crystal. I got
a very nice response with a bandwidth something like 900 Hz,
and ultimate attenuation of at least 110 dB. I reduced all the
crystal loads to 50 ohms, and the bandwidth narrowed to about
500 Hz. This general idea was discussed long ago, based on an
HP design that varied the loads with PIN diodes in order to
change the bandwidth. But it also is a nice simple design to
get a narrow bandwidth which you can adjust during assembly to
get your target bandwidth. For real-world crystals, the
frequencies of the crystals can be adjusted to identical values
with series capacitors, and there is no reason that the final
response should have any ripple whatsoever.
It appears that the 500 Hz buffered filter could be done with 4
crystals and still get good response. This would require only 3
amps, which could be tiny inexpensive op amps, in order to
achieve good power supply rejection. One stage could have gain
to eliminate the filter loss.
Sam W.
----
| Hi
Sam,
As a side note, if planning to add gain within a filter, you could actually eliminate the need for the I.F. Amplifier in the MSA. Just make the total gain of the "Amplifilter" about 35 dB. Scotty |
Crystal Ladder Filters
That would be a good idea if all my filters had this design, but I'm only going to do it for the narrowest. It could work for wider filters, but you would have to add more crystals.
I think I have found the optimal approach: Create two 2-crystal filters. Connect them with a buffer amp. This basically doubles the dB values of attenuation at every point, without creating any resonance interaction between the two filters, so each pair can be independently tuned. Connect 50-ohm source and load, and load the two inner crystals with 50 ohms. If you like what you get, adjust the amp gain to reduce the loss. If you want a broader bandwidth, then all the 50-ohms need to be increased (which will also reduce the loss). Because the amp is in the middle, it probably can only be used to offset the loss of the first half of the filter; otherwise the second half might get overloaded.
In simulations, it appears that if a crystal is mis-tuned, the loss increases and a small bump appears on the side of the response. Mis-tuning never seems to create ripple on the peak. Ripple only arises if the coupling capacitors between each pair of crystals are too small (i.e. too much coupling). So if you see ripple, you know exactly what capacitor to adjust and which way to adjust it.
Tuning a crystal is done with a series capacitor. Reducing the capacitance increases the crystal frequency. The idea is to get all crystals to the same frequency. If they are close to begin with, maybe no tuning is required.
The circuit does not seem very sensitive to input and output reactances. I put shunt 10 pF on the input and saw no change.
Sam W.
------------------
---------